@Ral Partha... The Parabolic Function is rotated around the line x=y. Your example is rotating both around the current x-axis and subtracting one volume from the other... this wont work for this problem as the radius used to integrate is not perpendicular to the x-axis, rather it is perpendicular to the line x=y about which the region is rotated.
@Ronster... One method, would be to rotate the reference axis so that it aligns with the function x=y. Easy enough to integrate when the parabolic function is rotated about the axis right? Wrong, this will change your parabolic function to something rather not pleasant to integrate by hand. Remember rotating the axis changes your limits of integration as well.
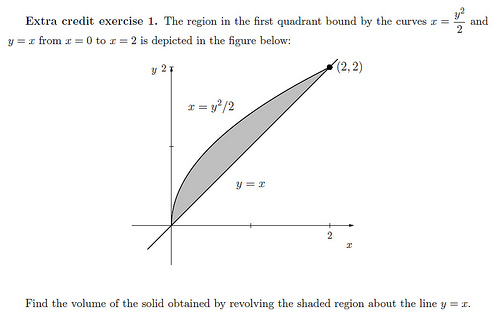
Noticing that the function x=y is offset 45 degrees from the x-axis, rotate the reference axis 45 degrees and change the equation of your parabolic function. This is done by substitution, x=x' and y=y', where x'=(x+y)/sqrt[2] and y'=(x-y)/sqrt[2]. By substituting these variables and solving for x gives the new form of the parabolic function.
x=(y^2)/2
(x+y)/sqrt[2]=(((x-y)/sqrt[2])^2)/2 ----- Substitue
x=-(sqrt[2^(11/2)*y+16]-2^(3/2)*y-4)/2^(3/2). ----- Solve
Your limits of integration will now be y=0 to y=sqrt[2^2+2^2]
Volume = Integrate {Pi*R

^2 dy}
Volume = Integrate {Pi*(-(sqrt[2^(11/2)*y+16]-2^(3/2)*y-4)/2^(3/2))^2 dy}
Volume = Evaluate {Sqrt[2]*y+y^2/2-(1/3+(2*Sqrt[2]*y)/3)*Sqrt[1 + 2*Sqrt[2]*y] } from y=0 to y=2.828427
Volume = 0.592384392 cubic units
One method to solve your problem...